TRABALHO PRÁTICO Nº 4 - MÉTODOS DE INTERPOLAÇÃO

MÉTODOS DE INTERPOLAÇÃO

OBJECTIVO

Pretende-se construir uma carta de precipitação com o menor erro possível, tendo por base o ficheiro vectorial rain.vct. O ficheiro contém dados referentes à precipitação em duzentas e sessenta e duas estações na região do Sahel, na África.

INTRODUÇAO

A carta de precipitação construída descreve a precipitação da zona oeste do deserto do Sahel. A zona é caracterizada por uma savana e estende-se da costa oeste à costa este africana, atravessando os seguintes países: Senegal, Mauritânia, Mali, Burkina-Faso, Níger, parte norte da Nigéria, Chade, o Sudão, Etiópia, Eritreia, Djibouti e Somália. O território recebe entre 0 e 300 mm anuais de precipitação, principalmente na estação do monção. A chuva caracteriza-se pelo seu ciclo anual e decanual. Existe uma forte correlação entre a chuva caída no Sahel e uma intensa actividade de furacões no Atlântico. Na figura 1 está localizada a zona do Sahel.

Figura 1 – Localização do Sahel

A partir do ficheiro base, rain.vct, será construída a carta de precipitação. Pode-se constatar, através da figura 2, um aumento de precipitação de norte para sul, consoante aproximação à zona tropical, e de este para oeste, conforme aproximação à zona litoral.

Figura 2 – Registo de precipitação nas 262 estações

Para a realização deste trabalho foi tido em conta o conceito de interpolação, isto é, pontos próximos no espaço tendem a ter valores mais semelhantes do que pontos mais afastados. O conceito de interpolação é útil quando os dados disponibilizados para uma zona são insuficientes, sendo estimados os dados em falta através dos disponibilizados. Existem quatro métodos interessantes que englobam o conceito de interpolação, estes são: polígonos de Thiessen, análise de tendências, Kriging e inversão do quadrado da distância.

Os polígonos de Thiessen transferem dados pontuais para áreas. Para se obterem polígonos de Thiessen unem-se todos os pares de pontos com segmentos recta e traça-se a perpendicular a cada segmento de recta.

A análise de tendência mostra tendências em larga escala de dados ou padrões dos dados. É um interpolador global e estatístico que ajusta os dados existente a um polinómio de x grau. Traduz-se em resultados fiáveis quando existe uma relação sólida entre o parâmetro e as variáveis.

O método Kriging baseia-se na taxa de alteração de variância com a distância entre pontos observados. Quando aumenta a distância a um ponto de medição de um atributo, aumenta a probabilidade dos valores desse atributo serem diferentes. É um interpolador estocástico. Por último, a inversão do quadrado da distância é um método de interpolação baseado no cálculo das médias móveis. Este método estima valores onde não existem pontos, utilizando uma média pesada dos pontos circundantes, em função da distância. Esta relação é inversamente proporcional, uma vez que, quanto maior a distância, menor o peso que tem na média, e quanto menor a distância, maior o peso.


METODOLOGIA

Na realização do trabalho, foi usado o programa Idrisi, no qual foram aplicados quatro métodos de interpolação para estimar os valores de precipitação desconhecidos.

Figura 3 – Metodologia geral adoptada

Através do comando POINTRAS, foram introduzidos os valores relativos ao ficheiro vectorial. Posteriormente foram aplicados os métodos de interpolação.

Serão determinados os erros médios pontuais para cada uma das superfícies interpoladas, com o intuito de seleccionar o método de interpolação com maior fiabilidade para a estimação pretendida. Para o cálculo dos erros foi considerada a seguinte tabela:

Método de elaboração de histogramas

A partir do ficheiro rain.vct, altera-se o Reference System para PLANE. Através do comando Reformat – RasterVector, obtém-se um histograma deste ficheiro em formato raster. Para a obtenção do histograma é necessário ter uma máscara vazia. Com o comando initial, em Data entry, estabelecem-se as características da máscara: 100 colunas e 80 linhas. O sistema de referência utilizado é PLANE.

Figura 4 – Fluxograma da metodologia adoptada na obtenção do histograma

O histograma criado provê a distribuição estatística dos dados.

A distância entre classes (Class width) deve ser a mesma para comparação de histogramas. Por defeito, o valor escolhido pelo idrisi é de 2,28 (figura 5). Porém, para melhor visualização será escolhido o valor 5. Os valores no eixo dos X – valores da precipitação serão aproximadamente entre 0 e 228. No eixo dos Y estão representados os valores dos píxeis.

Figura 5 – Image histogram

Através do histograma (figura 6) pode-se verificar uma distribuição de precipitação mais elevada aproximadamente nas estações 165 e 180.

Figura 6 – Histograma relativo à distribuição dos valores de precipitação

MÉTODOS DE INTERPOLAÇÃO

1. ANÁLISE TENDÊNCIA – TREND

A análise de tendência é um método de interpolação que permite ajustar um polinómio de valores observados, com o valor estimado a partir destes. A variável distribui-se no espaço em função das coordenadas, ou seja, a variável independente são as coordenadas geográficas e a variável dependente é a precipitação.

Para a análise de tendência, utiliza-se o comando TREND, em Gis Analysis – surface Analysis – interpolation, figura 7. Pretende-se uma análise de tendência cujo histograma se aproxime com o primeiro. Deste modo é possível modificar a ordem do polinómio, obtendo um histograma próprio para cada ordem.

Figura 7 – Trend surface analysis

A figura 8 apresenta a metodologia adoptada para a análise de tendência.

Figura 8 – Fluxograma da metodologia adoptada na Análise de tendência

Em seguida, são apresentados os mapas de análise de tendência linear, quadrática e cúbica.

Figura 9 – Análise de tendência: linear

No mapa de tendência linear, os valores de precipitação aumentam de Nordeste para Sudoeste, não variando significativamente na linha Este-Oeste.

Figura 10 – Análise de tendência: quadrática

No mapa de tendência quadrática, os valores de precipitação aumentam de Nordeste para Sudeste, sendo no geral mais elevados a Oeste que a Este.

Figura 11 – Análise de tendência: cúbica

No mapa de tendência cúbica, os valores de precipitação aumentam de Noroeste para Sudeste e no geral são constantes de Este para Oeste.

O mapa de interpolação escolhido para a análise de tendências é o quadrático, pois embora tendo um coeficiente de correlação inferior ao mapa de análise cúbica, consegue-se reconhecer um padrão (função adaptável) no seu histograma, não se verificando tal facto na analise de tendência cúbica ou superior. Os valores dos coeficientes para a análise de tendência linear, quadrática e cúbica são de 79,15; 84,19 e 86,03% respectivamente.

Numa regressão linear, com o aumento do grau do polinómio, o valor de R2 a ela associado aproxima-se à unidade, dado a recta de tendência progredir para 100% nos gráficos. No entanto, é necessário que se verifique um padrão no histograma e tal facto não acontece na análise de tendência cúbica. Tal facto pode ser confirmado nos histogramas das figuras 12 e 13.

Figura 12 – Histograma: Análise de tendência quadrática

Figura 13 – Histograma: Análise de tendência cúbica

2. INVERSO DA DISTÂNCIA PESADA (1/D): INTERPOL

Este método tem por base a relação entre os valores e a distância, os valores de precipitação obtidos relacionam-se com os valores pontuais do ficheiro vectorial rain dependendo dos valores vizinhos, logo pontos próximos no espaço tenderão a ter valores de precipitação mais parecidos que pontos mais afastados.

A figura 14 representa a metodologia adoptada para o método inverso da distância pesada.

Figura 14 – Fluxograma da metodologia adoptada no Inverso da Distância Pesada

Utiliza-se o commando INTERPOL, Gis Analysis – surface Analysis – interpolation, figura 15. Na janela INTERPOL, em distance weight expoent estabelece-se o peso que a variável terá, ou seja, o expoente da distância.

Figura 15 – Surface interpolation

Após aplicação do modelo, são criados dois mapas de inverso da distância pesada, linear e quadrático.

Figura 16 – Inverso da distância pesada: linear

Figura 17 – Inverso da distância pesada: quadrática

Pode-se constatar que a precipitação, em ambos os mapas, cresce no sentido Noroeste-Sudeste. Para cada mapa está associado o seu histograma correspondente, figuras 18 e 19.

Figura 18 – Inverso da distância pesada: Histograma linear

Figura 19 – Inverso da distância pesada: Histograma quadrática

3. POLÍGONOS DE THIESSEN

Para a realização deste método é necessário converter o ficheiro RAIN em formato vectorial, para formato integer. A metodologia adoptada está representada na figura 20.

Figura 20 – Fluxograma da metodologia adoptada na obtenção de Polígonos de Thiessen

Foi utilizado o comando THIESSEN, Gis Analysis – surface Analysis – interpolation.

Figura 21 – Thiessen polygon

A partir deste método de interpolação, verifica-se que na área em questão, os valores de precipitação são iguais ao valor pontual de onde se determinou a região (polígono) mais próxima a esse mesmo ponto (figura 22).

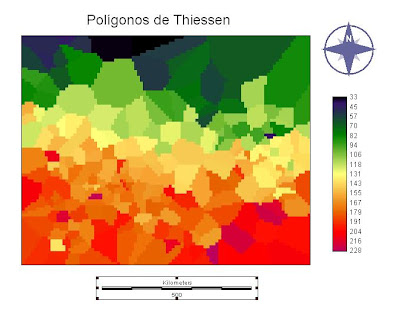
Figura 22 – Polígonos de Thiessen

Apresenta-se também o histograma correspondente aos polígonos de Thiessen, na figura 23.

Figura 23 – Histograma de Polígonos de Thiessen

A precipitação aumenta de Norte para Sul e mantém-se aproximadamente constante de Este para Oeste, embora existam alguns pontos que contrariam a tendência global do parâmetro.

4. VARIOGRAFIA E KRIGING

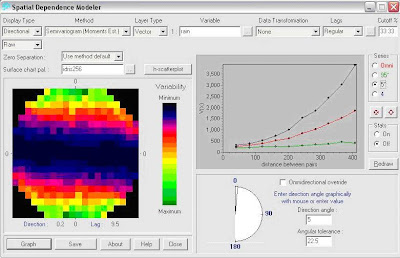
O método de Kriging é um método de interpolação que se baseia na diferença da variância com o aumento da distância entre dois pontos. Para a realização do Kriging, recorre-se ao menu Gis analysis, Surface analysis, interpolation e abre-se a janela Spatial Dependence Modeler. Inicialmente, o Display Type está em Surface. O gráfico traduz a nuvem do variograma, designada pela forma como os valores da semivarância estão dispostos no espaço. A distância que corresponde a um lag zero encontra-se no centro, a partir do qual as distâncias dos lags vão aumentando em todas as direcções.

Para analisar as direcções em que a variabilidade espacial ocorre, constroem-se variogramas direccionais. DisplayType altera-se para directional, residuals altera-se para raw e selecciona-se Omnidirectional override, para obter o variograma omnidireccional (a vermelho) como demonstra a figura seguinte. A figura abaixo apresenta também os variogramas direccionais a 95º, a verde, e 5º, a preto, direcções perpendiculares.

Figura 24 – Spatial Dependence Modeler – variogramas omni, 95º e 5º

Pode-se observar no variograma omnidireccional três comportamentos espaciais diferentes, três tipos diferentes de crescimento da curva, segundo a distância dos pontos. Estas diferenças são visíveis nos duzentos e trezentos kilómetros. Possivelmente existam três padrões diferentes de variabilidade, dependentes de factores associados à região.

Para obtenção do gráfico H-scaterplot, selecciona-se lag1 e Graph Lag (figura 25).

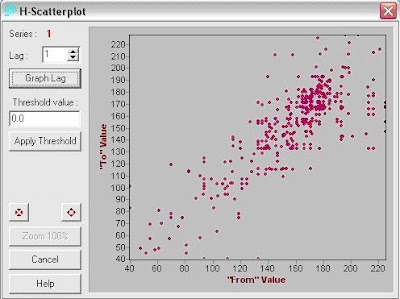
Figura 25 – H-Scatterplot

O gráfico mostra os pares de dados relativos aos valores de precipitação. Uma correlação dos pontos no espaço revela uma linha de 45º. Quanto menor for a correlação, mais dispersa será a distribuição dos pontos.

Posteriormente procede-se à selecção do modelo matemático que descreve o padrão da variabilidade espacial – Model Fitting. Selecciona-se o comando kriging and simulation (figura 26). Escolhe-se a opção Block Average Variogram Values, e estabelece-se o tamanho em X e Y de 20 para a sua interpolação. Este número refere que a interpolação vai resultar numa estimativa média para um conjunto de 20x20 píxeis. É também necessário obter uma máscara (matriz) vazia, cujo valor do raio é 1.

Figura 26 – Model fitting

Figura 27 – Kriging and simulation

Após aplicação do modelo, são obtidos dois mapas, um referente à precipitação -superfície com os valores estimados para toda a região - e outro referente aos erros (mapa relativo à superfície com as variâncias estimadas), figuras 28 e 29.

Figura 28 – Mapa de Kriging: precipitação

A precipitação aumenta de Noroeste para Sudeste, sendo difícil definir em que direcção é constante devido à distribuição das zonas correspondentes aos diferentes valores de precipitação.

Figura 29 – Mapa de Kriging: erros

O erro aumenta consoante a quantidade de pontos disponíveis na área pretendida. Ao analisar o ficheiro vectorial rain, verifica-se que a zona localizada a Nordeste no mapa não tem muitos pontos para os quais se possa interpolar informação, logo o erro associado será muito superior ao das restantes regiões do mapa.

ANÁLISE COMPARATIVA

1. ANÁLISE DAS SUPERFÍCIES INTERPOLADAS

São comparados os resultados obtidos com os dados vectoriais proporcionados de modo a cumprir o objectivo do trabalho.

Comparando os histogramas da análise de tendência com o histograma dos dados vectoriais da precipitação, pode-se inferir que o histograma da análise de tendência quadrática é semelhante ao histograma dos dados vectoriais, logo o modelo quadrático é o escolhido.

A análise de tendência linear fica totalmente descartada, pois os histogramas não têm qualquer semelhança.

Figura 30 – Comparação do histograma dos dados vectoriais com os histogramas da análise de tendência

Em relação ao inverso da distância pesada, pode-se inferir que, ambos os histogramas apresentam uma distribuição da precipitação muito semelhante, tendo um pico máximo na mesma classe que o histograma dos dados vectoriais. Porém, a escolha recai sobre o histograma quadrático, pois quanto maior o grau do valor da distância, maior o peso que esta terá no valor obtido.

Figura 31 – Comparação do histograma dos dados vectoriais com os histogramas do inverso da distância pesada

Relativamente aos polígonos de Thiessen, o histograma não tem semelhanças com os dados vectoriais. O facto de a partir de valores pontuais construir áreas faz com que os histogramas não se assemelhem.

Figura 32 – Comparação do histograma dos dados vectoriais com o histograma de polígonos de Thiessen

2. VALIDAÇÃO

Para proceder à validação do modelo mais adequado, utilizaram-se os dados da tabela 3.

Na eleição do melhor método de validação para a construção da carta de precipitação, foram calculados os erros associados a cada método (tabela ER).

Pode-se verificar que, da análise de tendência, o método que aufere um menor erro médio associado é a análise de tendência quadrática, como já tinha sido confirmada através da interpretação dos histogramas. Porém, este método não é o que possui um menor erro associado. Como era de esperar, o método de interpolação ao qual se associa um erro mais elevado é o método polígonos de Thiessen, pois tratam da construção de área.

Pode-se constatar que o método com um menor erro é o inverso da distância pesada, tendo um valor de erro médio de 104, face aos 137 do método Kriging, aos 114 da análise de tendência quadrática, e aos 644 dos polígonos de Thiessen.


CONCLUSÃO

Como conclusão e com o intuito de responder ao cerne da questão, na selecção do melhor método de interpolação foram analisados os erros médios associados. Pode-se inferir que, o método com menor erro médio associado será provavelmente (não contabilizando outros possíveis factores de alteração) o melhor método para a construção da carta de precipitação.

Verifica-se então que, o melhor método dentro da análise de tendência foi a quadrática. No entanto, este não foi o método com menor erro médio associado de entre os quatro apresentados.

Métodos como polígonos de Thiessen são descartados pois para além de ser um interpolador abrupto, apresenta um aumento da precipitação de uma forma não contínua, formando áreas (polígonos) onde todos os pontos são de igual precipitação. Esta afirmação pode ser contrastada com o elevado erro associado a este método.

É de notar que, o método Kriging costuma ser um bom modelo para a construção deste tipo de cartas, pois para além de ser um interpolador estocástico, permite avaliar incertezas e erros associados, produzindo superfícies suaves devido ao seu carácter gradual. No entanto, o erro médio associado é superior ao erro médio associado para o inverso da distância pesada, concluindo assim que neste caso, não é o melhor método.

Como conclusão final, assinala-se o método do inverso da distância pesada como o mais favorável à construção da carta de precipitação no Sahel, tendo um erro médio associado de 104. Este interpolador é local, determinístico e exacto e como já foi indicado, a distância actua como peso, permitindo ajustar esse mesmo peso através do expoente.


REFERÊNCIAS BIBLIOGRÁFICAS

- SILVA, Renato S. & ALMEIDA, Regina C. – Métodos Numéricos Interpolação/aproximação. Laboratório Nacional de Computação Científica. 2003.

- SEIXAS, Júlia – Métodos de interpolação: geoestatísticas. Análise de variogramas. Kriging. Universidade Nova de Lisboa – Faculdade de Ciências e Tecnologia. 2006-2007.